くじを引く順番で当たる確率は変わる?


あるお店でくじ引きをやっていました。
10本のうち1本が当たりです。

くじを引こうと10人の人がならんでいます。

10人のうちだれか一人だけ「あたり」を引けるんだね。

先頭の人から順番にくじを引いていくと、5番目の人が「あたり」を引いて、くじ引きは終了しました。

「あたり」が出たってことは、残りは全部「はずれ」だから、くじ引きはそこで終わりになったんだ……


残りの5人は不満そうです。
「くじを引いてもいないのにハズレだなんて…」
「もっと早く来てならべばよかった」

たしかに…
くじを引いてないのに「はずれ」って残念……

10人のうち何番目にくじを引けば一番当たりやすいと思いますか?

5番目か6番目かな? なんとなく…

どうでしょう…
みなさんも考えてみてくださいね。
↓ここをおすと開きます

1番目の人がくじを引こうとする時、10本のくじの中の1本が当たりです。

このとき確率(かくりつ)という言葉を使って「1番目の人が当たりを引く確率は10分の1です」のように言うことがあります。
確率とは、ものごとがどれぐらい起こりやすいかを数字で表したものです。
この場合、1番目にくじを引く人がどれぐらい「あたり」を引きやすいかを数字で表すと「10分の1」といえるということです。
確率は中学校以降でくわしく習いますので、サラッと読んでいただければと思います。

2番目の人がくじを引こうとする時、1人目の人が引いた後なので、残っているくじは9本。9本のくじの中の1本が当たりです。

2番目の人が「あたり」を引く確率は9分の1……かな?

どうでしょうか…もう少し見ていきましょうね。
3番目の人がくじを引こうとする時、1人目と2人目の人が引いた後なので、残っているくじは8本。8本のくじの中の1本が当たりです。

「あたり」を引く確率は8分の1…??
あれ? どれぐらい「あたり」を引きやすいかを数字で表したのが確率だよね?
後に引いた方が当たりやすいの?

同じように考えていくと、10番目の人がくじを引こうとする時、残っているくじは1本です。
その1本が当たりです。


10番目の人は絶対に当たりを引く…!
やっぱり、後に引く人の方が「あたり」を引きやすいっていうこと?
でもなんかおかしい……

そうですね。なんだかおかしいです。
もう一度、2番目の人について考えてみましょう。


2番目の人が「あたり」を引くためには、
・1番目の人が「はずれ」をひく
・2番目の人が「あたり」をひく
この両方がそろわなくてはいけません。


1番目の人が「はずれ」をひく確率を考えましょう。
10本のくじのうち9本が「はずれ」なので10分の9です。

さらに2番目の人が当たりを引く確率が9分の1です。
確率の計算の仕方は中学校以降で習います。くわしい説明ははぶきますが、この場合次のようにかけ算をします。
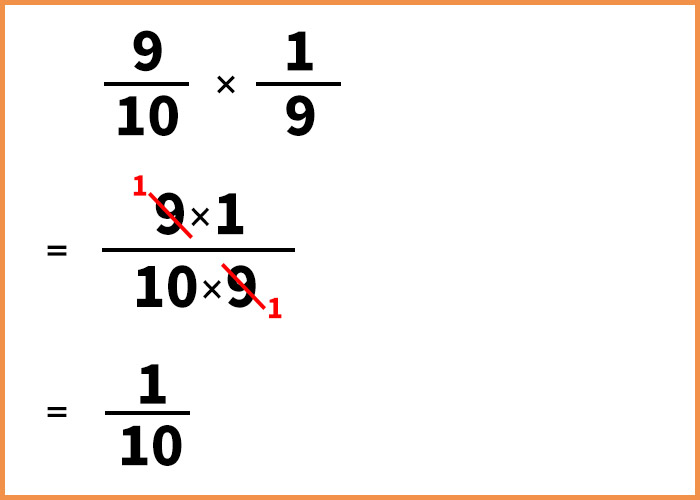

計算をすると、2番目の人が「あたり」を引く確率は10分の1となります。

10分の1……
1番目の人と同じだね!

3番目の人が「あたり」を引くためには、
・1番目の人が「はずれ」をひく
・2番目の人が「はずれ」をひく
・3番目の人が「あたり」をひく
これらがそろわなくてはいけません。

1番目の人が「はずれ」を引く確率は10分の9だったね。
2番目の人が「はずれ」を引く確率は……


残っているくじは9本。そのうち8本が「はずれ」
2番目の人がはずれを引く確率は9分の8かな?

そのとおりです!
さらに、3番目の人が「あたり」を引く確率は…


残っているくじは8本。そのうち1本が「あたり」…
3番目の人が「あたり」を引く確率は8分の1……?

よくわかりましたね!
確率の計算方法についてくわしい説明ははぶきますが、次のようにかけ算をしますよ。
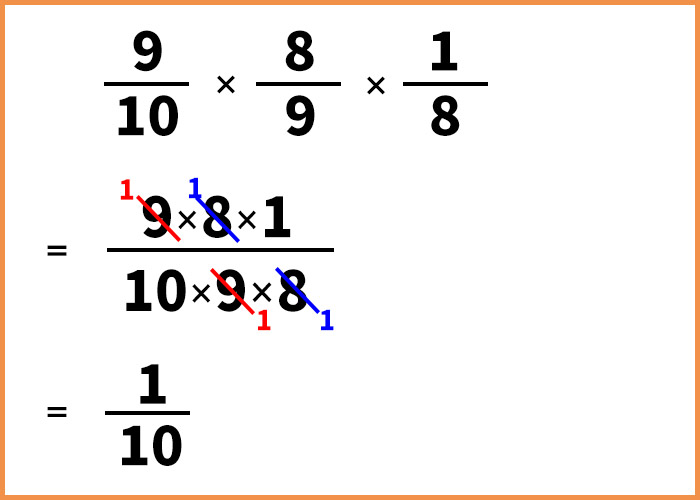

また10分の1!
1人目、2人目、3人目…みんな同じ……

同じように10番目の人についても考えてみましょう。
1番目から9番目までの人が外れを引いて、なおかつ10番目の人が当たりを引く確率を考えるといいですね。
ちょっとむずかしいですが、次のような計算になりますよ。
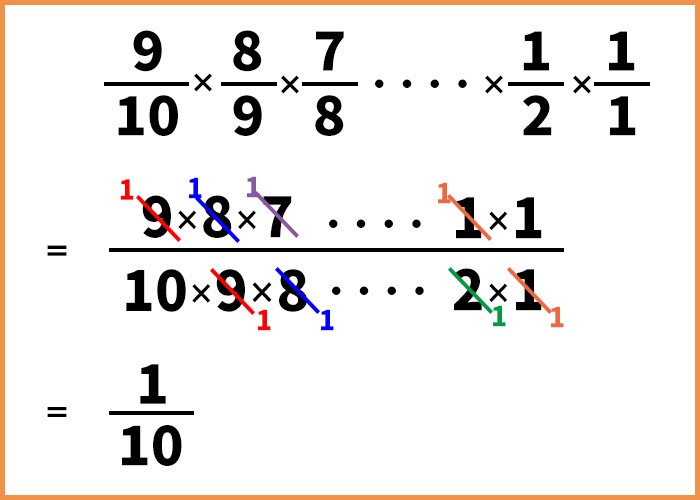

やっぱり10分の1だ!
1番目から10番目まで、みんな「あたり」を引く確率は10分の1なんだね

そうなんです。
何番目にくじを引いたら一番当たりやすいか、わかりましたか?

何番目にくじを引いても、当たりやすさは同じだね!

















ディスカッション
コメント一覧
まだ、コメントがありません