円周の長さの問題をもっと解いてみよう
円周の求め方の基本問題が解けるようになったら、次は応用問題にも挑戦してみましょう。これも、５年生後半から６年生向けの内容です。
- 円周の長さを求める応用問題を解こう
円周の長さを求める問題で、もっと基本的な問題練習をするノートの説明記事はこちらです。
https://homework-recipe.com/5thsan7円、半円、おうぎ形の、周囲の長さを求める問題が解けるようになり、もう少し難しい問題をやってみたい時におすすめなのが、今回の自主学習ノートです。
円周の長さを求める応用問題
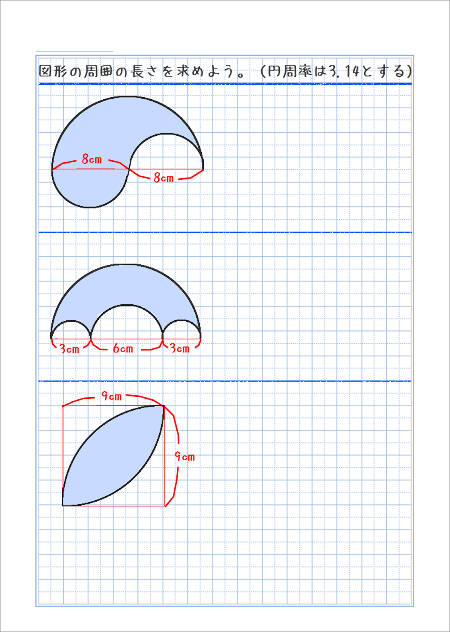
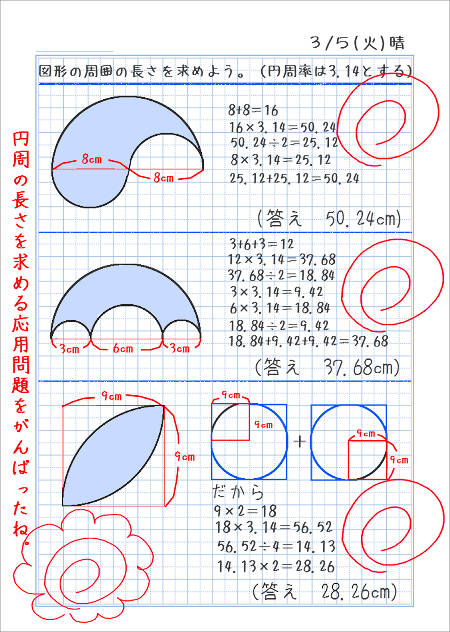
三つの図形を描き、図形の周りの長さを求める問題を解いてみましょう。
式を書き、答えを求めましょう。筆算は計算用紙を別に用意するか、隣のページに筆算を書いてもいいと思います。
この下に、解説入りの画像があります。問題を解き終えてから、ご覧下さい。
（上の画像の、青い解説の文字は、ノートに書かなくてもいいと思います。また、緑色の点は、図形を描く時に、コンパスの針をさすところです）
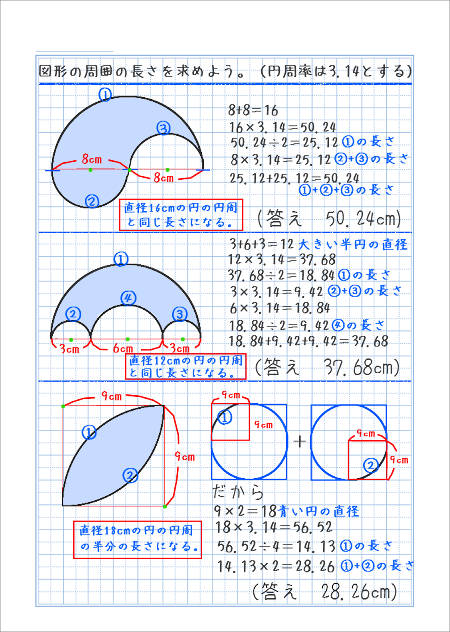
式の例と答えを書いています。ここでは基本的な方法で解いた場合の式を書きました。
- 直径を求める
- 直径に3.14をかけて、円周の長さを求める
- 円周を２で割り、半円の弧の長さを求める（いちばん下の問題は、４で割る）
この組み合わせだけで解く場合の、式を書いています。
この問題をもっと速く解くためには、次のことを覚えます。
上の画像で、赤い四角で囲ったところに書いたように、上の２問は、答えが、大きい円の円周の長さと同じになるのです。
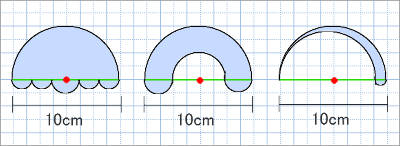
↑この画像で、緑の線を直径とする場合、図形の周囲の長さは、どれも、直径10cmなので、
10×3.14＝31.4cm となります。
面積は全く違います。面積の求め方 半径×半径×3.14 と、混同しないように気をつけましょう。
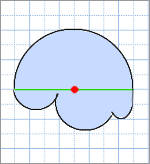
周囲の長さが、大きい円の円周の長さと同じになるのは、大きい円と、小さい円の直径がすべて重なっている場合だけです。下のような図形は、直径が重なっていなかったり、半円になっていない部分があったりするため、円周と同じにはなりません。
こういったことを覚えておくと、式の途中を省略でき、速く解くことができますが、基本的な解きかたをまずはしっかり覚えましょう。
答え合わせをして、親が確認し、コメントを書くとこのようにノートが完成します。
まずは、この画像の式と答えに書いたような、円周の求め方の基本を組み合わせて解けることが大切です。
