合同な三角形をかこう

2015年7月13日2022年4月1日

合同な三角形を３つの方法で描く自主学習ノートの例をご紹介します。

ぴったり重ねあわせることができる２つの図形を、合同な図形といいます。一方をうら返しにしてぴったり重ねあわせることができる場合も、合同であるといいます。

1. 合同な三角形を３つの方法で描いてみよう

三角形の場合は、辺の長さと角の大きさのうち、次のことを使って合同な図形を描くことができます。

1. ２つの辺の長さと、その間の角
2. １つの辺の長さと、その両はしの角の大きさ
3. ３つの辺の長さ

三角形の辺の長さや角の大きさのうち、上のどれかがわかれば合同な三角形を描くことができるということです。

それでは、自主学習ノートの作り方を説明していきます。

合同な三角形をかく自主学習ノート

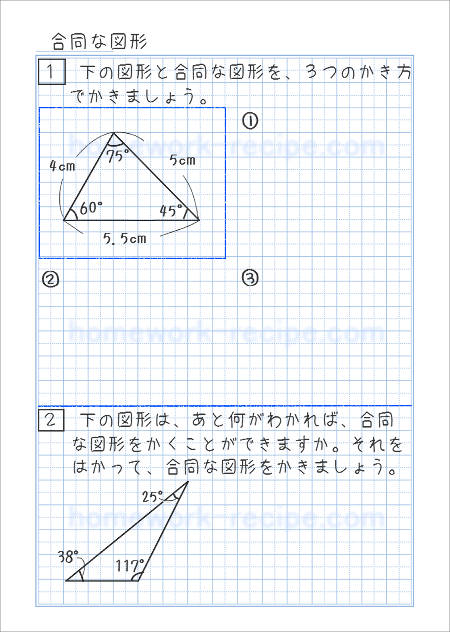
３つの辺の長さと、３つの角の大きさがわかっている三角形を１つ描きます。これと合同な三角形を、３種類の方法で描いてみましょう。

ノートの下の方には、辺の長さと角の大きさの一部だけがわかっている三角形について、あと何がわかれば合同な図形が描けるかを考え、それを定規や分度器で測り、合同な図形を描く練習問題をすることにします。

下の問題は、３つのかき方のうちどれで描くこともできます。そのうちの１つを選び、定規や分度器で測って、合同な図形を描いてみてください。

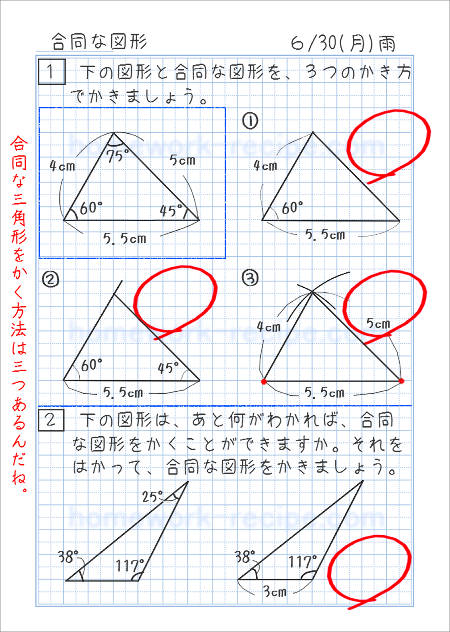
３種類の描きかたは、このようになります。

1. ２つの辺の長さと、その間の角

　…長さのわかっている１つの辺を描き、分度器で角度を測ってもう１つの長さのわかっている辺を描く。頂点をつないで３つ目の辺を描く。

2. １つの辺の長さと、その両はしの角の大きさ

　…長さのわかっている１つの辺を描く。その両はしから、分度器で角度を測って２つの辺を描く。２つの辺がまじわるところが頂点となる。

3. ３つの辺の長さ

　…長さのわかっている１つの辺を描く。その辺の両はしを中心として、コンパスで、残り２つの辺の長さを半径とする円を描く。円がまじわったところが頂点となる。（画像では、赤い点で円の中心を示してありますが、これは自主学習ノートにはかかなくてもいいです）

こんな学習もしてみましょう

三角形だけではなく、四角形、五角形、円などの合同な図形を描いてみましょう。

また、四角形は、１本の対角線で２つの三角形に分けられます。また、２本の対角線で４つの三角形に分けられます。正方形、長方形、台形、平行四辺形、ひし形と様々な四角形について、対角線で分けることによって、合同な三角形ができるのはどれかを調べてみましょう。