円の周りの長さを計算しよう
円周率を使って、円の周囲の長さを計算する自主学習ノートを作りましょう。小数のかけ算を使います。５年生の後半から、６年生におすすめの自主学習です。
- 円、半円、おうぎ形の周囲の長さを計算する。
基本的な問題が解けるようになり、応用問題もやってみたい方におすすめのノートもあります。
https://homework-recipe.com/5thsan6いろんなパターンの問題に挑戦してみましょう。
ノートの作り方
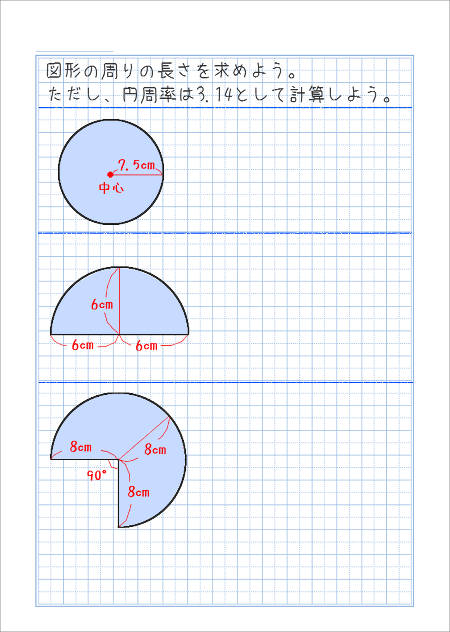
半径がわかっている円の円周を求める基本的な問題からやってみましょう。
２問目は、半円の周りの長さを求めます。
３問目は、円からおうぎ形を抜き取った形にしました。
半円の問題、扇形の問題は、円の弧の部分の長さだけを求めて答えとしないように、気をつけましょう。
３問目は、角度が90°の扇形が、円を４つにわけたうちの１つであるということを思いつけると、解けると思います。
解答と解説を書きこんだノートがこちらです。
３問目について補足します。
（青い文字で解説を入れていますが、これは自主学習ノートには書かなくてもいいと思います）
円を４つに分けたうちの１つが、90°の扇形です。ここでは円周を４で割ることで、弧の長さを求めました。
次に、それを引いた円周の残りの部分を求めましょう。
最後に、半径の長さの直線を２カ所、足すことを忘れないようにします。
また、分数のかけ算を習った後ならば、扇形の中心角90°は、円の360°の1/4（4分の１）なので、それを除いた、この図形の中心角は3/4（4分の3）ということから、
50. 24（円周の長さ）×3/4＝37.68（図形の弧の長さ）
と、１本の式で計算することもできます。
また、3/4は、小数にすると、0.75です。
50. 24（円周の長さ）×0.75＝37.68（図形の弧の長さ）
と小数どうしのかけ算で計算することもできます。
こんな自主学習もしてみましょう
直径から円周の長さを求められるようになったら、次のような自主学習もやってみてはどうでしょうか。
- 円周から直径や半径を求める
- 身の回りにある、円形や半円、扇形のものの周りの長さを計算する
- いろんな角度の扇形の、周りの長さを求める
- 直径と円の周りの長さの関係を、表やグラフに表す。
色々工夫して、取り組んでみて下さい。
