拡大図と縮図をかこう

三角形と四角形の拡大図や縮図をかく自主学習をやってみましょう。
- 三角形と四角形の拡大図と縮図をかく
まずは、拡大図、縮図とは何か、おさらいしておきましょう。
- もとの図と、拡大図(または縮小図)の角の大きさは同じ
- もとの図と、拡大図(または縮小図)の辺の長さの比が同じ
ということです。辺の長さも同じである場合は、合同な図形となりますね。
「辺の長さの比が等しい」とはどういうことでしょうか。
例えば、辺の長さが「6cm、4cm、4cm」の三角形は、辺の長さの比が「3:2:2」ですね。
辺の長さが「3cm、2cm、2cm」の三角形も、辺の長さの比が「3:2:2」で、上の三角形と、辺の長さの比は等しいです。
辺の長さが「12cm、8cm、8cm」の三角形も、辺の長さの比は「3:2:2」で、これも上の2つの三角形と、辺の長さの比が等しい図形です。
それでは、このような性質をもった拡大図や縮図を、実際に自分でかいてみる自主学習ノートの作り方をご紹介します。
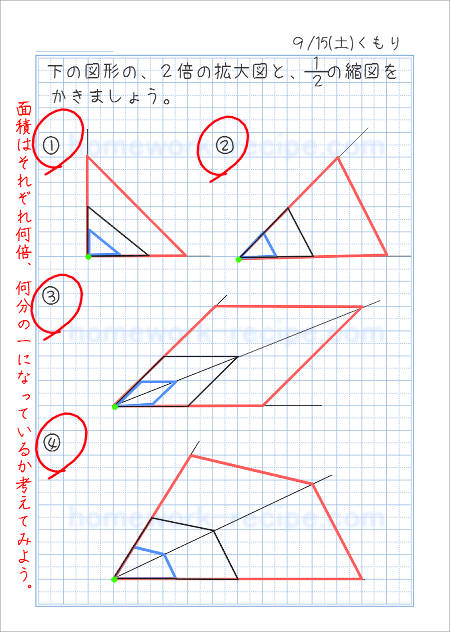
拡大図と縮図をかく自主学習ノート
問題文を書きましょう。
次に、拡大図と縮図のもとにする図形をかきます。

方眼のノートの場合、辺の長さは方眼を数えればわかる場合もありますが、定規で測ってかく方法を確認しておきましょう。
拡大図は、コンパスを使って辺の長さを測ってかいてもいいです。
黒のえん筆ですべてかいてもいいですが、縮図は青えん筆、拡大図は赤えん筆でかくなど、色を替えてかくと見やすいと思います。

ここでは、1つの頂点を中心に拡大、縮小する方法でかきました。中心とする点は、このノート見本では緑色で示してあります。この点はノートにはかかなくてもいいです。
かき方の手順の一例を説明します。
- 中心とする点から、辺をのばして線を引きます。
- 四角形の場合は、中心とする点と、向かい合う頂点を結んだ線(対角線)ものばして線を引きます。
- 辺の長さ、対角線の長さを2倍にしたところが拡大図の頂点となります。
- 辺の長さ、対角線の長さを2分の1にしたところが、縮図の頂点となります。
拡大図・縮図の他の問題
もとの図形を見て、拡大図や縮図をかく問題の他に、このような内容で自主学習をしてみましょう。
- いろいろな図形の中から、もとの図形の拡大図、縮図になっているものはどれかを選ぶ問題
- 縮図や拡大図の、角の大きさや辺の長さを計算で求める問題
また、どのような辺の長さでも、必ず拡大図や縮図の関係になる図形は何か、ということも習うので、復習しておきたいです。
- 正三角形、正方形など正多角形すべて
- 円
これらの図形は、どんな大きさでも、それぞれ拡大図や縮図の関係になります。正多角形は、辺の長さがすべて等しいので、辺の長さの比は当然同じになりますね。
他の図形は拡大図や縮図の関係になる場合と、ならない場合があります。丸暗記するだけではなく、どんな場合に、拡大図や縮図の関係になるか、図形を描きながら確認しておくと良いと思います。