並べ方と組み合わせ方-その２
今日は、並べ方と組み合わせ方の、もう１つのノート例を紹介します。
- 並べ方と組み合わせ方の練習問題
組み合わせ方について、これよりもう少し基本的な学習内容のノート例です。よろしければ、こちらもご覧下さい。
https://homework-recipe.com/6thsan3並べ方の問題と、組み合わせ方の問題の違いにも気をつけて問題を解いていきたいと思います。
数字カードの並べ方を調べよう
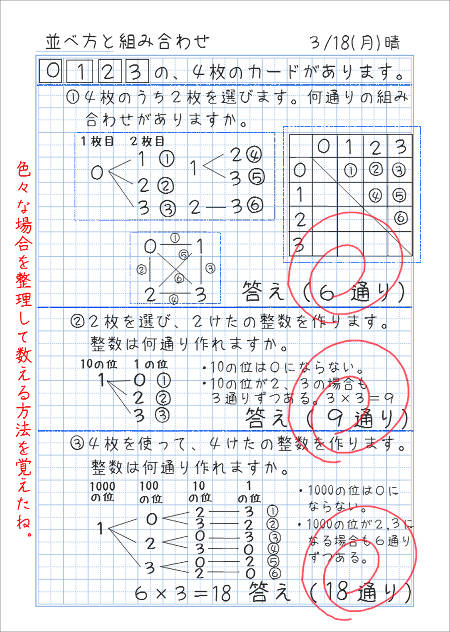
今回は、４枚の数字カードを使って、３つの問題を考えてみましょう。
ただ２枚を選ぶ場合と、並べて整数を作る場合では考え方が違うことに注意します。問題文を読み取る力も必要ですね。
ノートをどのように使うかを考え、罫線を引くなどして準備をします。下の画像のように、問題文を書きましょう。
組み合わせ方を考える方法は、以下のように色々あります。
- 樹形図を描いて考える方法
- 表を描いて考える方法
- 辺と対角線を書いて数える方法
とにかく全部書きだして、ダブっているものを消していく方法もありますね。←解法を思いつかない時、いざとなったらこれで。
②の問題は、10の位が１の場合と、２の場合、３の場合、どれも３通りです。３通り×３で９通りが答えとなります。
- 組み合わせを考える場合…
1-2と、2-1は同じことなので１つと数える。 - 並び方を考える場合…
1-2と2-1は別なので、２つと数える。
整数はいくつできるか、という問題は、並び方を考える問題ですね。（12と21は、同じ数ではない）
このノート見本では、考え方も詳しく書きましたが、もっと簡単に樹形図や表をさっと描いて、答えを書くだけでもいいと思います。
場合の数の学習
並び方や組み合わせのことを、場合の数といいます。中学以降でも習うので、中学受験でこの手のもっと難しい問題を速く解く必要がある方を除いて、ここで取り上げたような、樹形図を描き、数えて答えが出せる程度の問題ができていればよいと思います。
どういう考え方をしたらいいかさっぱりわからない、という時はとりあえず、１つでも２つでもいいので、問題文に書かれてある条件にあてはまる組み合わせや、並び方を、書きだしてみるといいと思います。
このノート見本で①の問題ならば、「２枚選ぶ？じゃあ『２と３』でしょ、『３と１』でしょ、『３と２』でしょ…あっ、『２と３』と『３と２』は同じか…」という感じで。
「全部で何通りとか言われても困る」と思うかもしれません。１つでもいいから書いてみると、糸口になるんじゃないでしょうか。
