割合の求め方【公式・くもわ・線分図】

このページでは、割合の求め方について解説します。
公式やくもわの図を使った基本的な解き方の他、線分図を使った解き方をくわしく解説しています。なぜそう計算するのかを納得しながら解ける、しかも学校で習うのと同じ途中式になる方法です。「割合が苦手」「解けるには解けるけどイマイチよくわからない」と困っている方はぜひ読んでみてください。
動画でも解説しています。
(16分51秒/BGM・ナレーションあり)
短い動画にまとめるために説明は早口で、省いたことも多いです。この記事では、動画ではぶいた説明も書いていますので、一つ一つ確認しながら進めたい方は、動画と合わせてこの記事をお読みくださいね。
割合が苦手になる理由
小学校で習う割合を、苦手とするお子さんも多いようです。
- 「もとにする量」「くらべられる量」といった用語がまずなじみにくい
- 文章題のなかで、どれがもとにする量で、どれが比べられる量なのか特定するのが難しい
- 覚えにくい公式をいくつも覚えないと解けないと思われている
- 覚えたところでどの公式を使うのか判断するのが難しい
- そもそも割合って何なのかがよくわからない
いろんな理由で、割合が苦手になってしまう人がいます。
割合の問題のよくある解き方

- 文章題を読み、「もとにする量」「くらべられる量」「割合」の3つの要素を見つける
- 3つの公式のうち、どれを使うのかを判断する
- 公式に数字をあてはめて計算する

公式を覚えるために、くもわの図と呼ばれるものが使われることもあります。
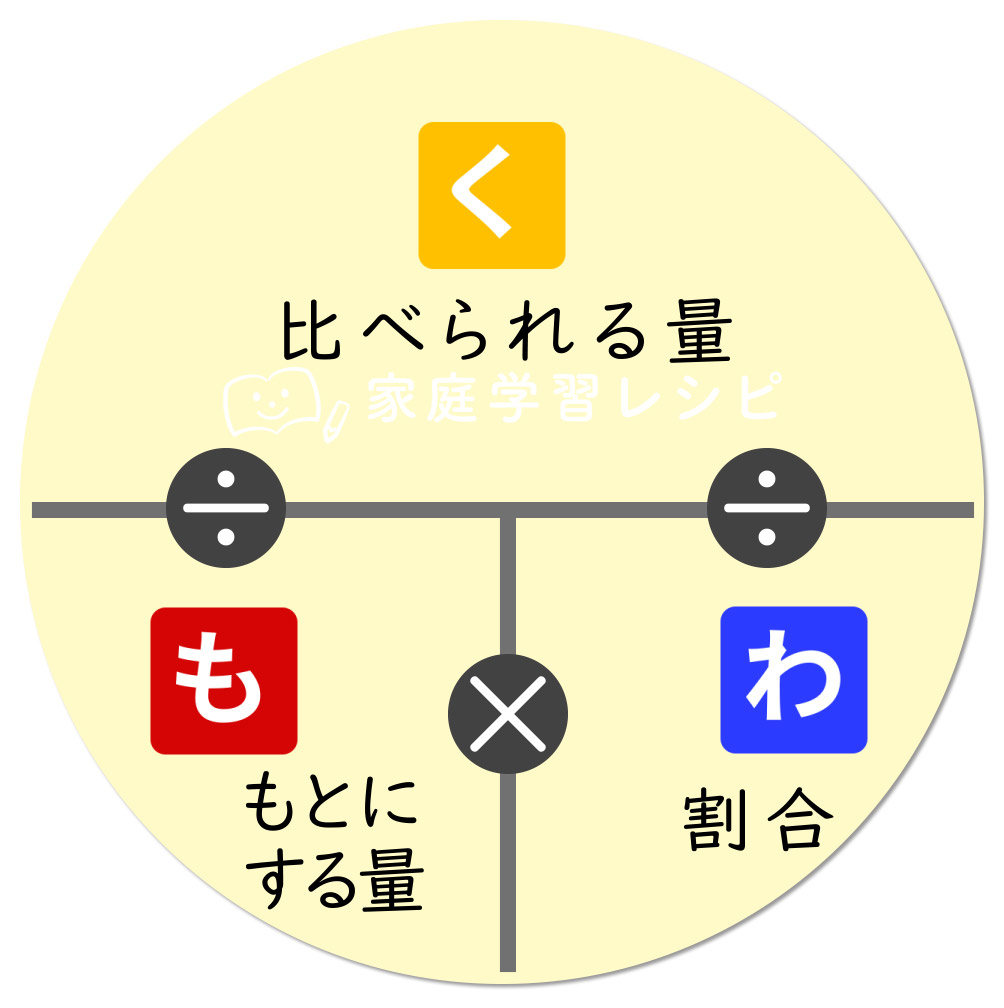
いちおうこれについても軽く説明しておきますね。
くもわの図で割合を求める公式を導き出す方法
- 割合以外の二つを使います
- 比べられる量ともとにする量の間にあるのは÷
- 上を下で割ります
割合=比べられる量÷もとにする量
くもわの図で比べられる量を求める公式を導き出す方法
- 比べられる量以外の二つを使います。
- もとにする量と割合の間にあるのは×なので二つをかけます。
比べられる量=もとにする量×割合
くもわの図でもとにする量を求める公式を導き出す方法
- もとにする量以外の二つを使います
- 比べられる量と割合の間にあるのは÷
- 上を下で割ります
もとにする量=比べられる量÷割合
この方法で解けて答えは合ったとしても、イマイチ意味がわからなくて、なんだか気持ち悪いと思うお子さんもいるのではないでしょうか。
割合の考え方は、中学以降で習う比例式、相似といった数学の考え方の基礎となります。できれば考え方を理解しながら解けることを目指したいものです。
そもそも割合とは何か
小学校の教科書では、このように説明しています。
もとにする大きさを1とみたとき、くらべられる大きさがどれだけにあたるかを表した数を、割合といいます
割合は何年生で習うのか
割合は、主に4~6年生で習います。その前に、2年生でかけ算を習う頃から、「~倍」という、割合の基礎となる考え方も学び始めます。整数の倍、小数の倍、分数の倍と、少しずつステップアップして、5年生でいよいよ本格的に割合を学びます。
さて先程書いた割合の定義ですが、文章の説明ではいまひとつよくわからないので、これをそのまま図に表してみましょう。
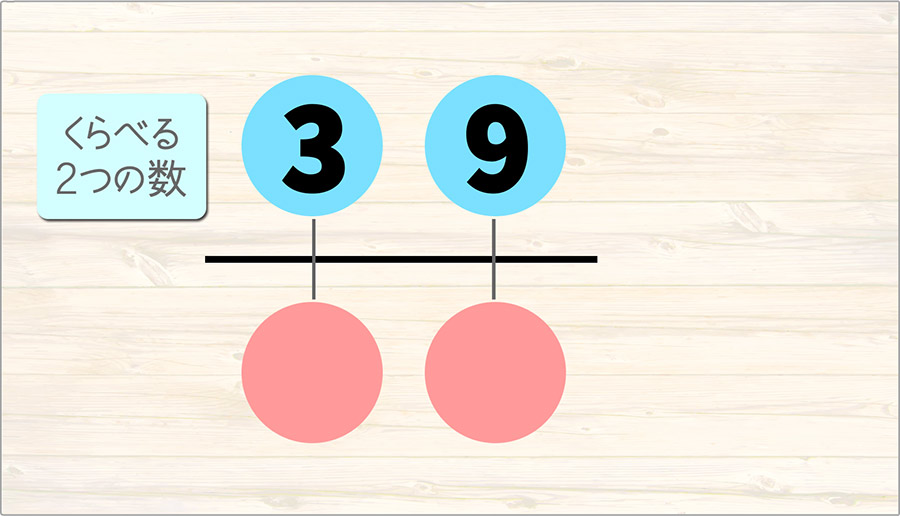
3と9という二つの数があります。
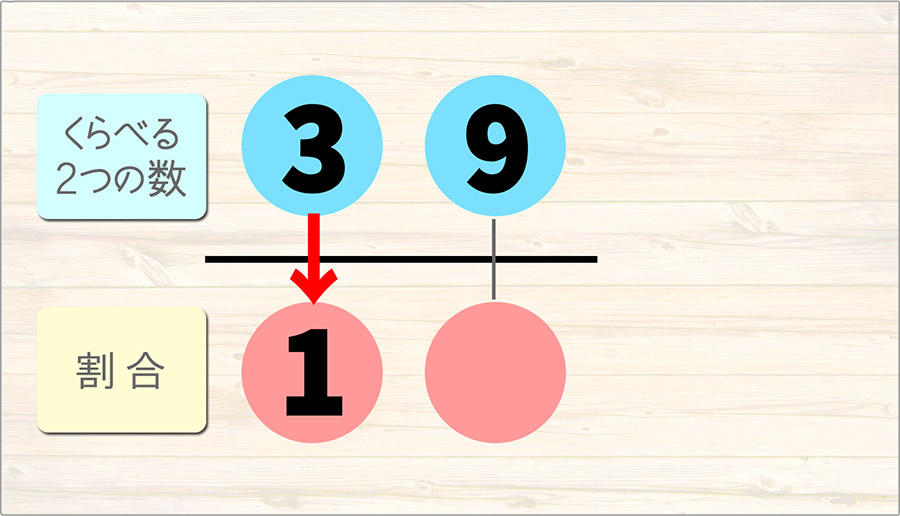
もとにする大きさ3を1とみたとき、
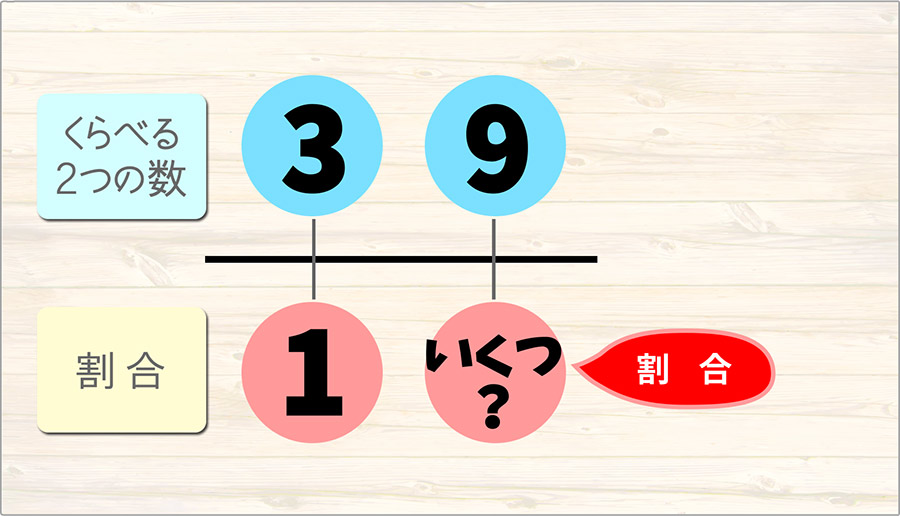
くらべられる大きさ9がどれだけにあたるかを割合といいます。
割合の説明をそのまま簡単な線分図にかいて、公式などを使わずに問題を解くことができます。
図をかいて問題を解く方法
図のかき方を説明していきます。
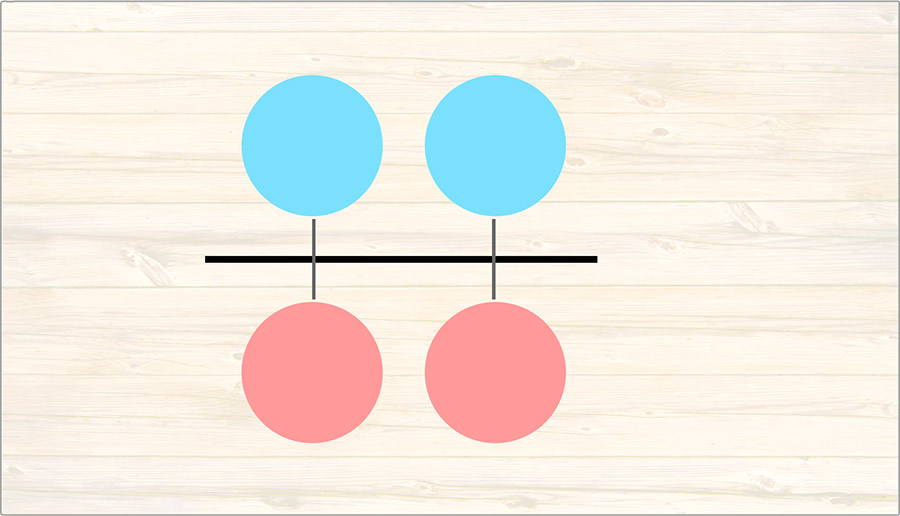
横棒は線分図をうんと簡略化したものです。
上に2つ、下に2つ、数字を書くところがあります。

線の上には、比べる二つの数を書きます。ここでは3と9を比べるので3と9を書いています。
線の下には、1と割合を書きます。3を1とみるので、3の下に1を書きます。

線の上下に4つ、数字を書く場所がありますが、問題文を読んで、1の他に2つの数字を書き入れることができれば、残りの1つは計算で求めることができます。

3を1とみたとき、9がいくつになるか(=割合)を求めてみましょう。
割合を求めてみよう
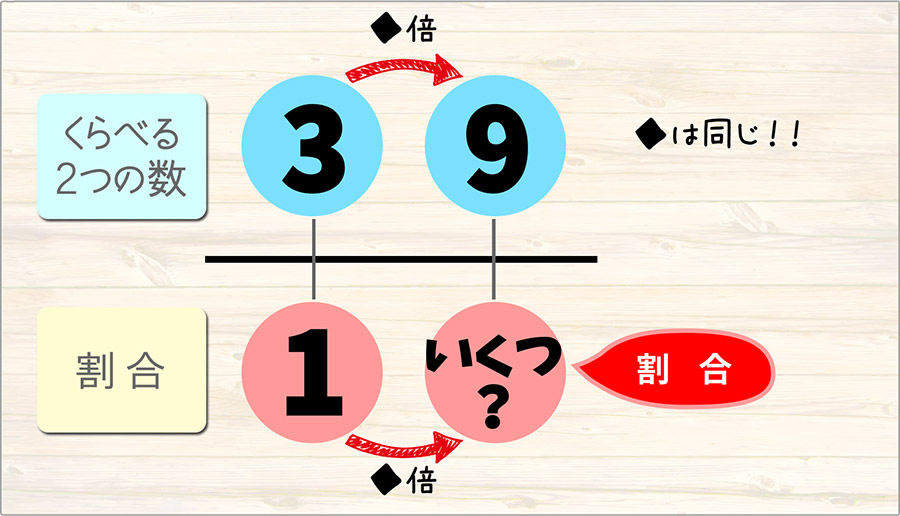
赤い矢印の向きに、数字が何倍になるかは、上と下で同じです。これは割合の大事なルールです。
このルールを使って、計算します。
9は3の何倍か?を求めるには、
9÷3=
を計算します。
9÷3=3
9は3の3倍ということです。
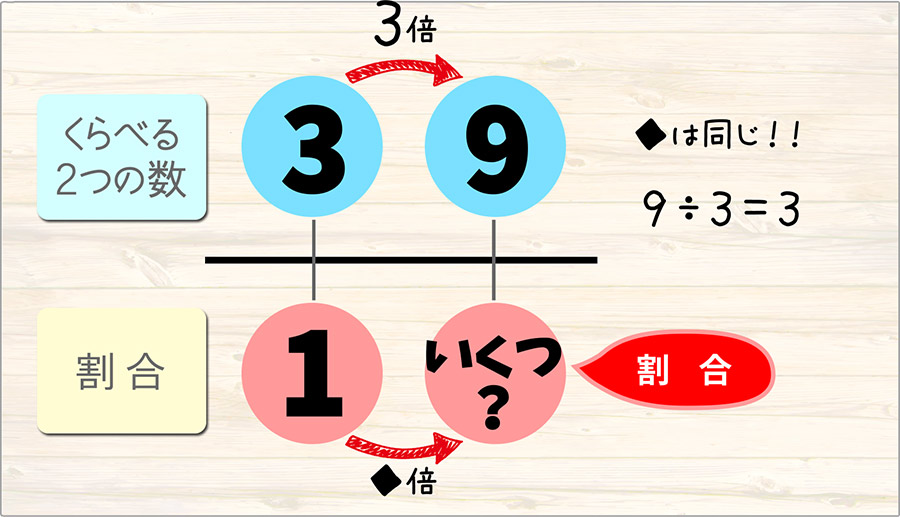
上下の矢印の向きと「何倍」になるかは同じなので、下の矢印も3倍になります。
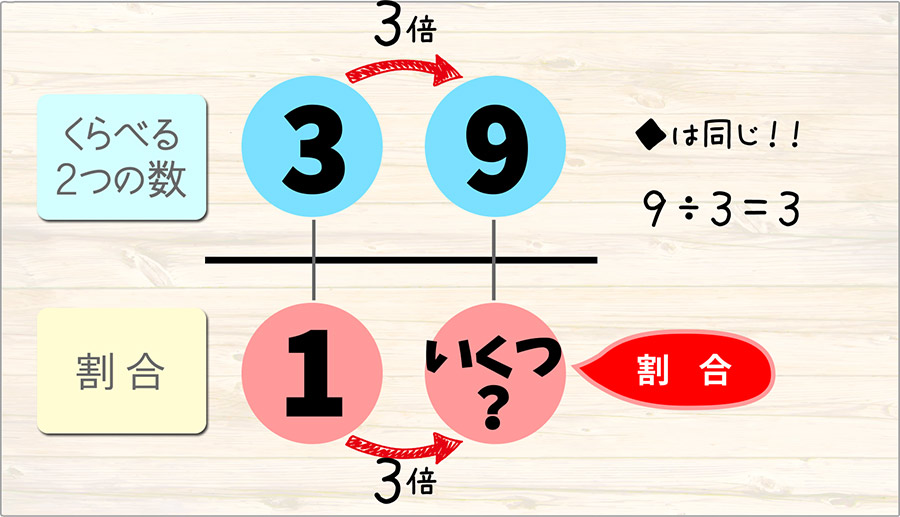
1の3倍ですから、右下のまるには3が入ります。
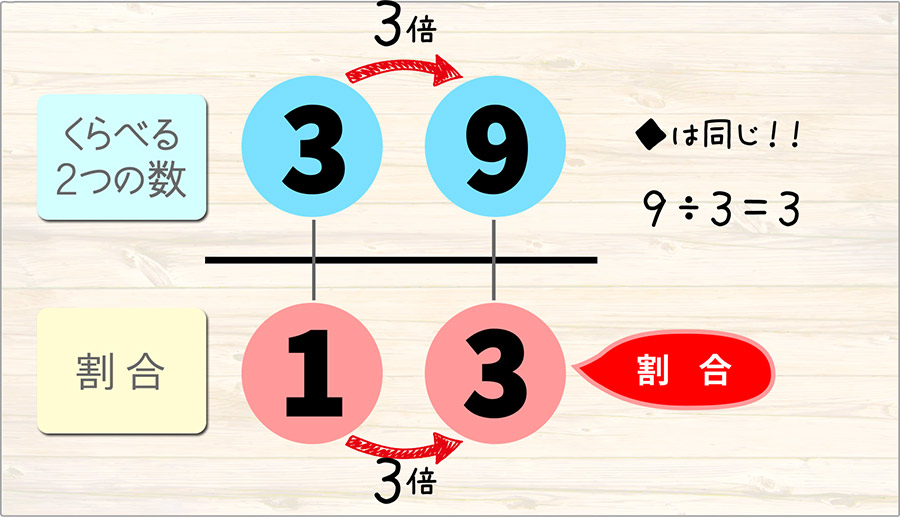
割合は3となります。
- 9は3の3倍です
- 3を1とみた時、9は3になります
- 3をもとにすると、9の割合は3です
- 3:9=1:3
上記はぜんぶ同じことを言っています。
ちなみに

この図で、1の上にある数が「もとにする量」です。
1の横にある数が「割合」です。
残りのひとつが「比べられる量」です。
このページで紹介している、線分図を使って解く方法は、これらの言葉や公式を覚えなくても、割合の問題が、考え方を理解しながら解けます。
ただ、学校の宿題やテストでは、学校で習った方法で途中式や考え方を書かされる場合があるかもしれず、これらの言葉や公式を覚える必要はないとまでは強くいえません。
線分図を使って割合の基本問題を解こう
線分図を使って、割合の基本問題を3題解いてみましょう。
割合を求める問題
ねこが6ぴき、犬が15ひきいます。犬の数はねこの数の何倍ですか?
線分図をかきます。線の上には比べるふたつの数を書きます。
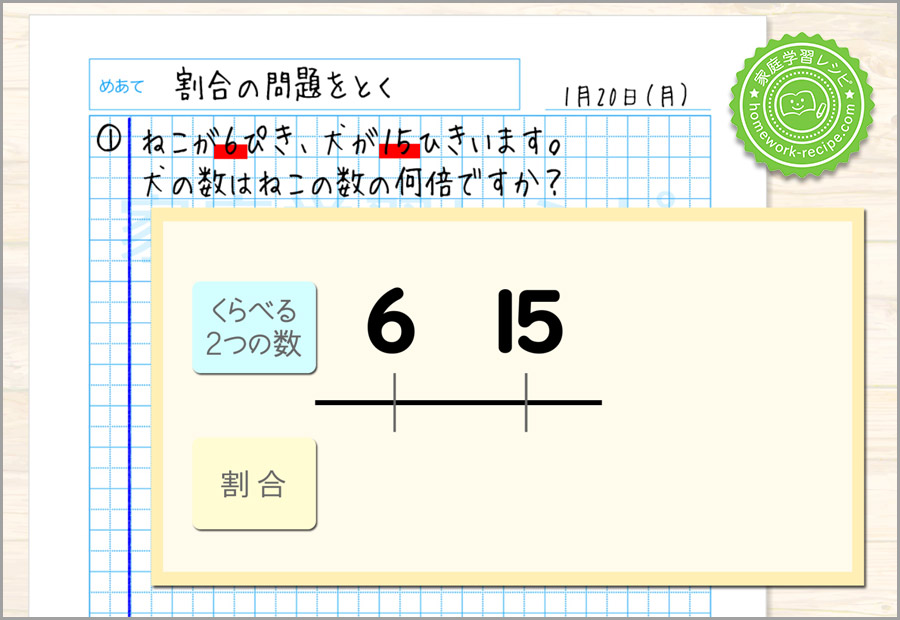
ここではねこと犬の数を比べるので、6と15を書きます。
線の下には1と割合を書きますが、どっちに1を書くかが大事です。
ねこの数6と、犬の数15のどちらを1とみて、ふたつの数を比べようとしているのかを、問題文から読み取りましょう。
1とみる数というのは、もとにする数のことです。
分かりにくい場合は、次のような手がかりを参考に考えてみましょう。

問題文の中から「●の何倍」というところを探してみると、「ねこの数の何倍」というところがありますね。

ねこの数、つまり6が1とみる数ですので、6の下に1を書きます。
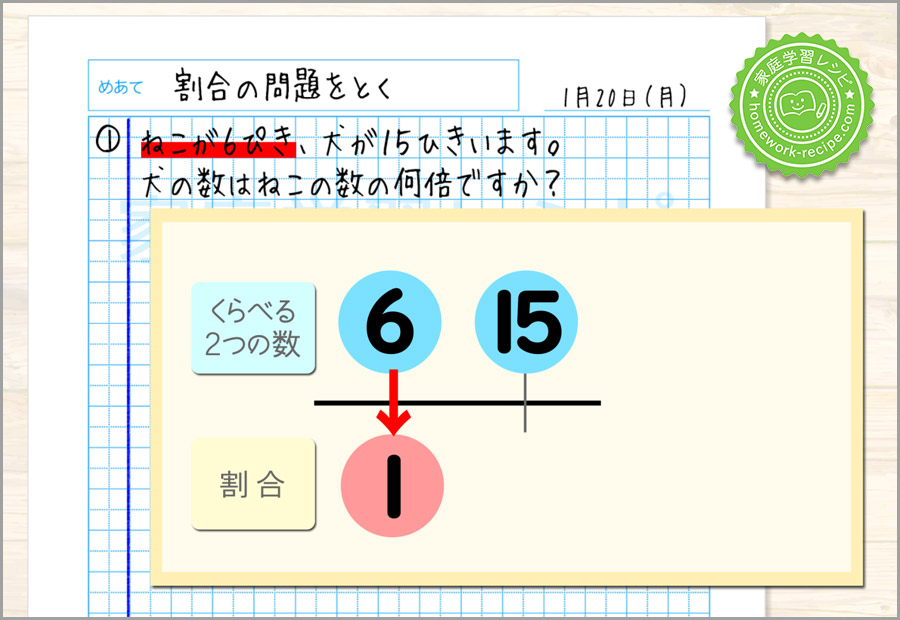
残りの一か所が割合です。
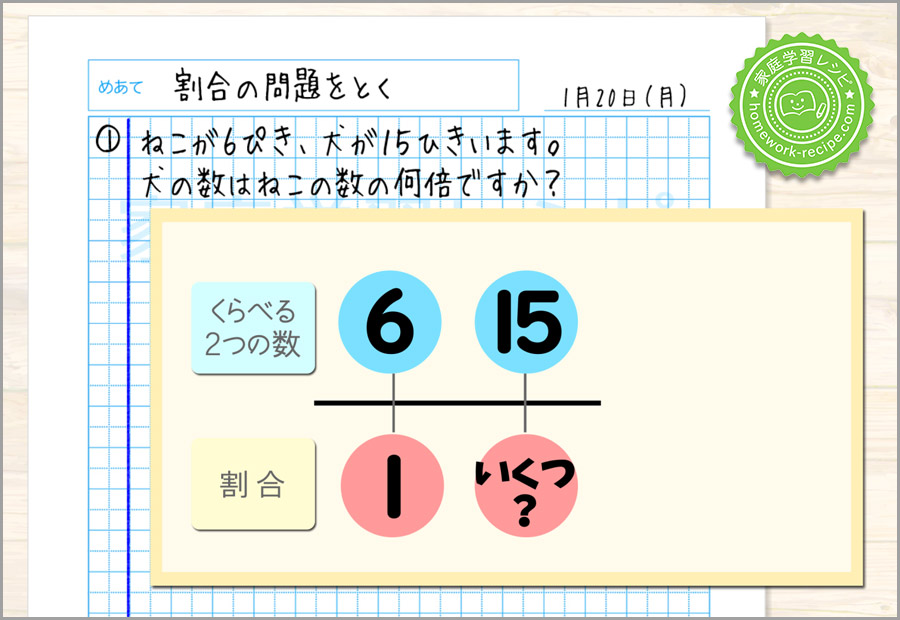
1の他に二つの数を書き入れることができれば、残りの一つは計算で求めることができます。
割合を計算で求めていきましょう。
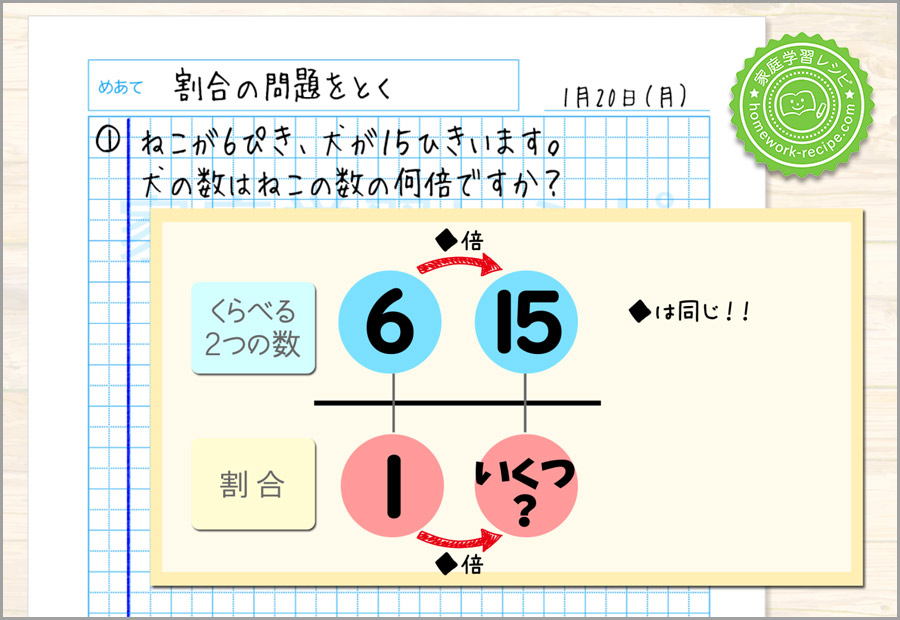
矢印の向きに上と下が何倍になるのかは、同じでしたね。
今回は上の数字が二つ入っているので、上が何倍になるかを計算できます。
15÷6=2.5
15は6の2.5倍ですね。
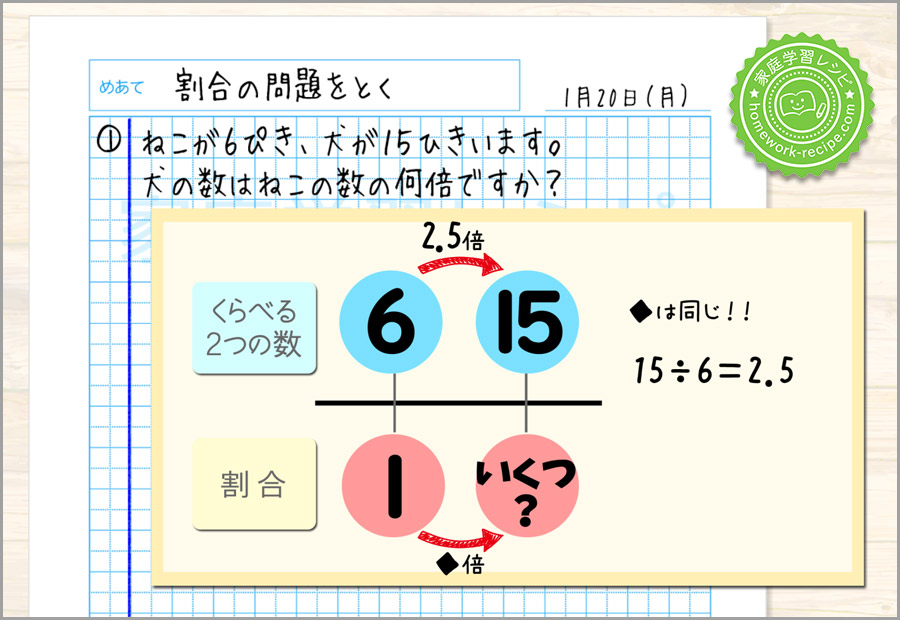
下の◆も同じ数字2.5が入ります。
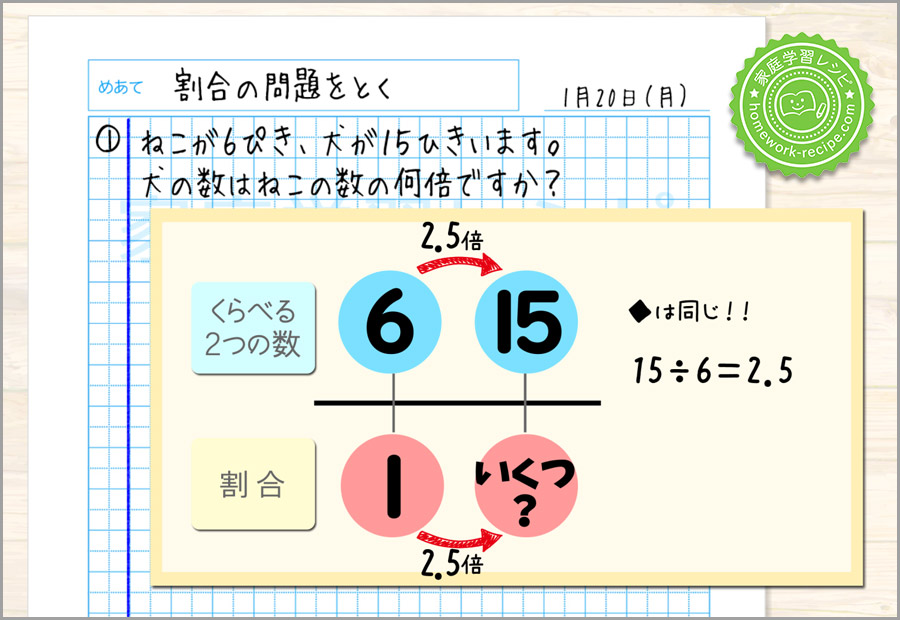
そして1の2.5倍なので、いくつ?のところにも2.5が入ります。
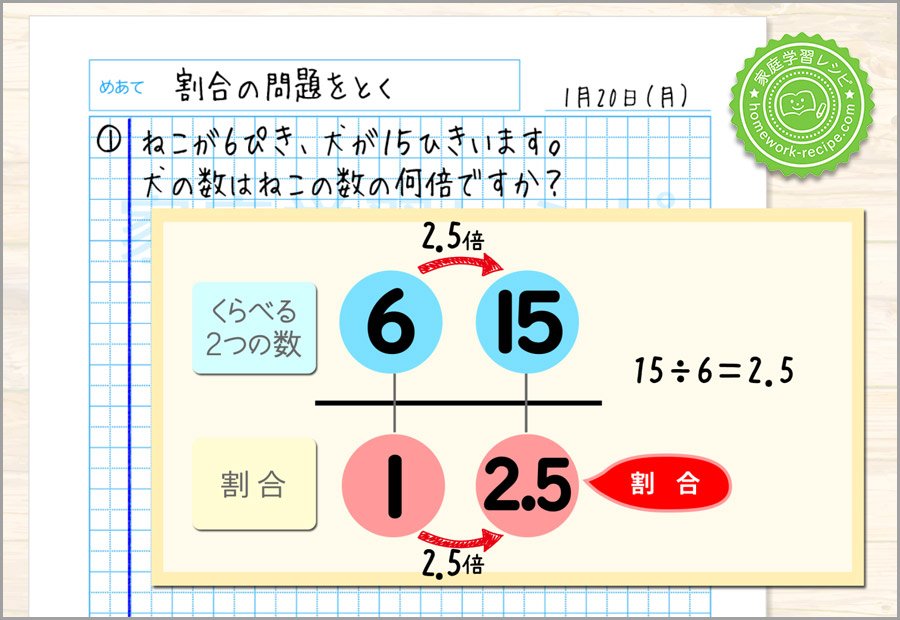
この2.5が割合で、問題の答えです。
答えは、2.5倍となります。
比べられる量を求める問題
女子の数は20人で、男子の数は女子の数の120%です。男子の数は何人ですか?
女子と男子の数を比べますが、女子の数だけわかっているので、線の上に女子の数20を書きます。
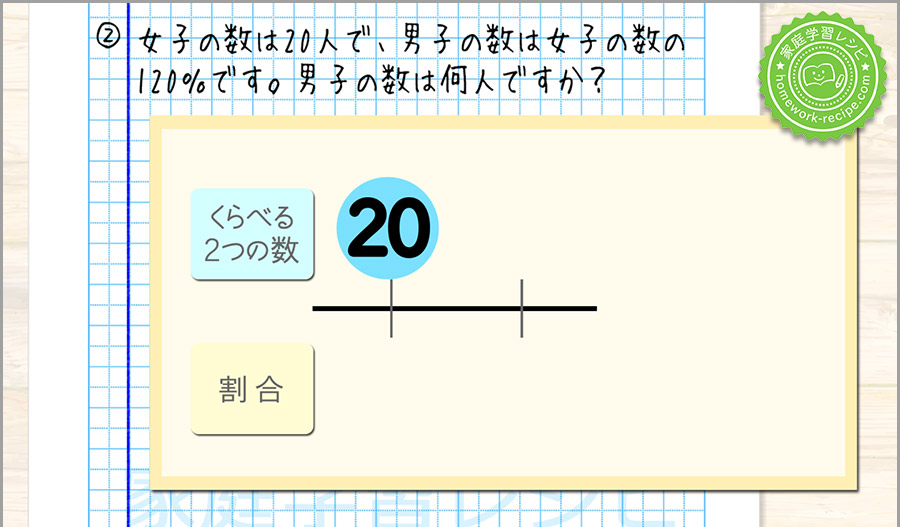
線の下には1と割合を書きます。
割合は120%で、1.2に直して計算します。
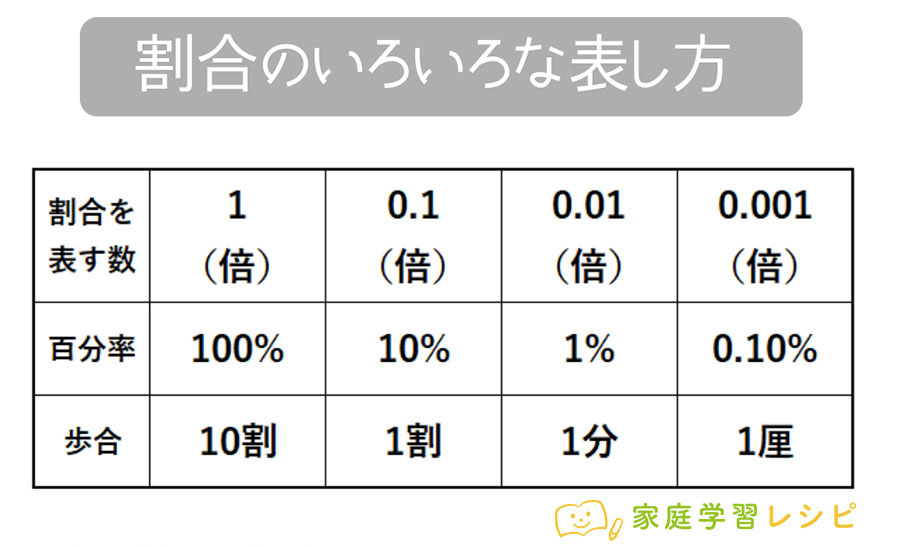
問題文から、女子と男子の数どちらを1とみて数を比べようとしているのかを読み取ります。わかりにくい場合は先程も出した手がかりを参考に…
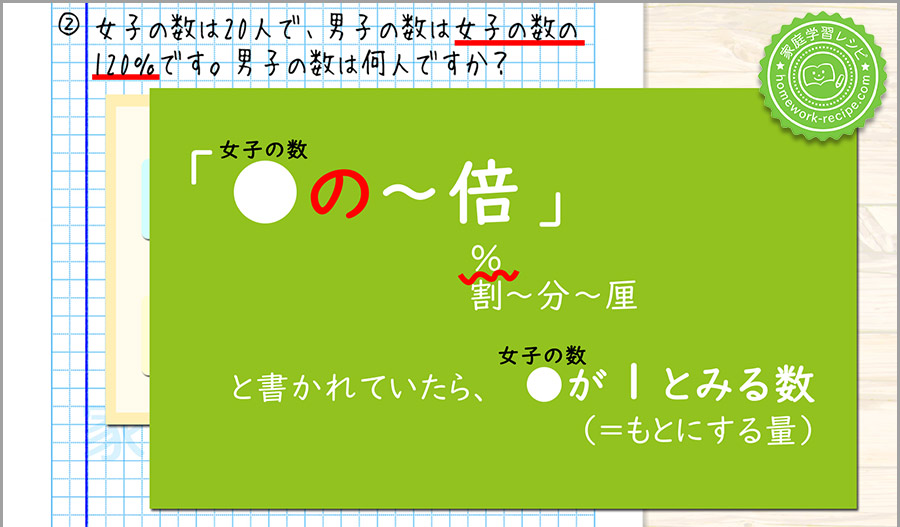
女子の数を1とみるということがわかるので、女子の数である20の下に1を書きます。
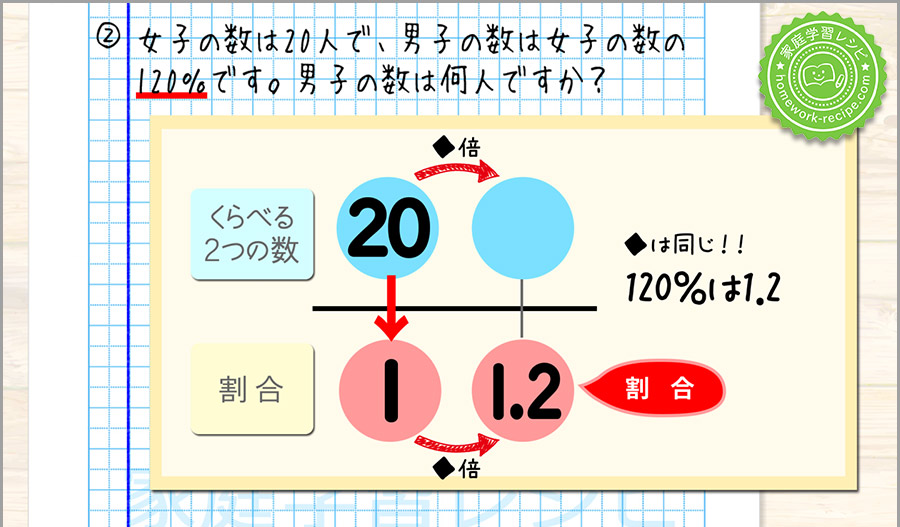
線の下のもう一方に、割合の1.2を書きます。
1.2は1の何倍か?を考えると1.2倍なので、下の◆に1.2が入ります。
上の◆も同じなので、1.2が入ります。
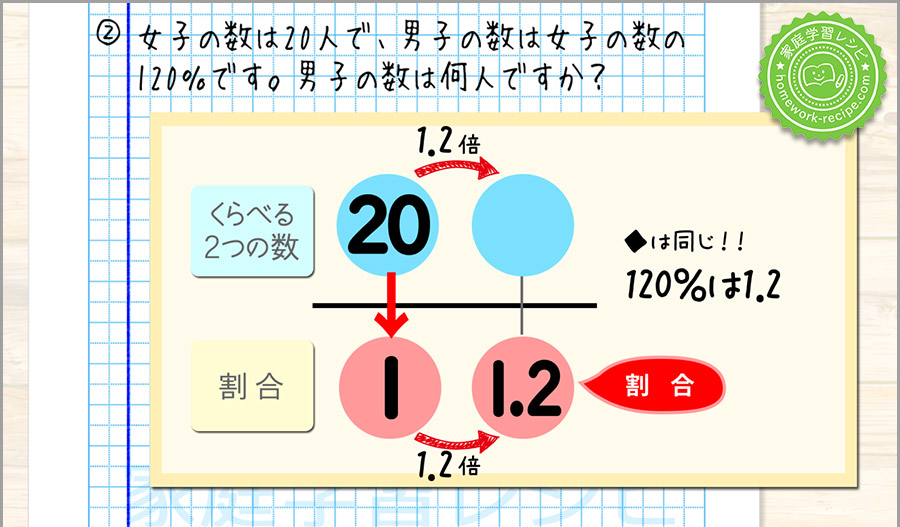
20の1.2倍を計算しましょう。
20×1.2=24
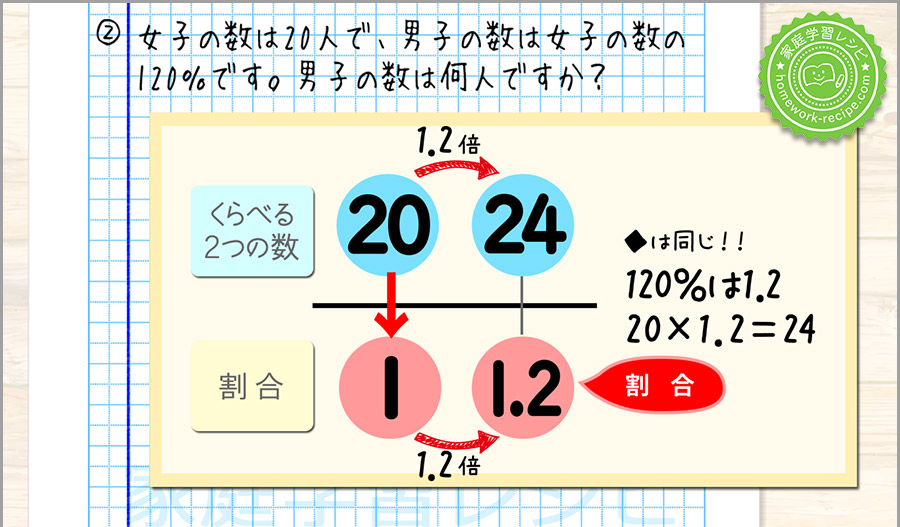
男子の数は24人というのが答えです。
もとにする量を求める問題
たかしくんの身長はお父さんの身長の8割で140㎝です。お父さんの身長は何cmですか?
たかしくんとお父さんの身長を比べます。
たかしくんの身長だけわかっているので、140を線の上に書きます。
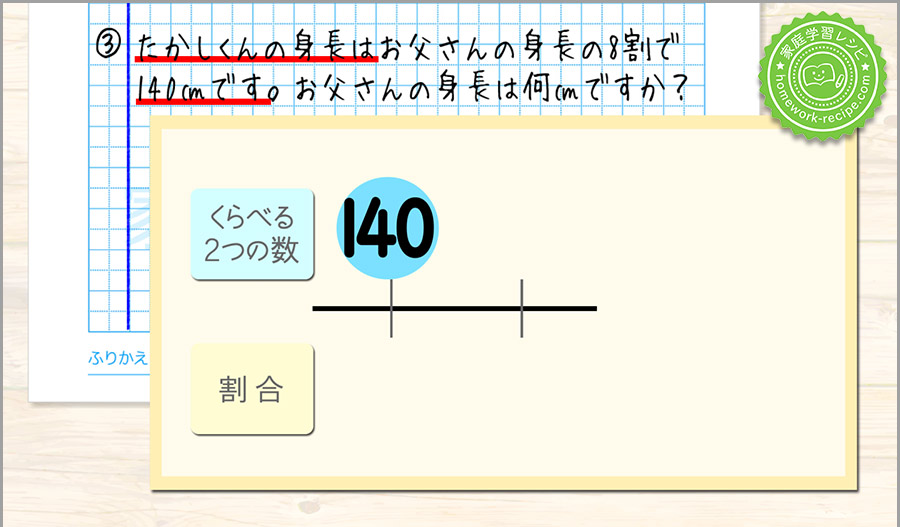
線の下には1と割合を書きます。
割合は8割です。0.8として計算をします。
たかしくんとお父さんの身長、どちらを1とみて比べようとしているのか、問題文から読み取ります。
分かりにくい場合は手掛かりを参考にします。
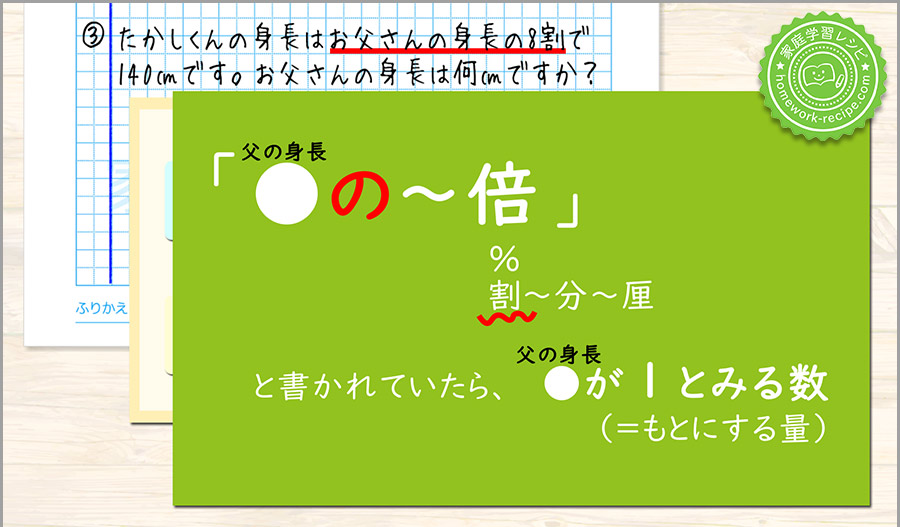
父の身長を1とみることがわかるので、父の身長の下に1、線の下のもう一方に割合である0.8を書きます。
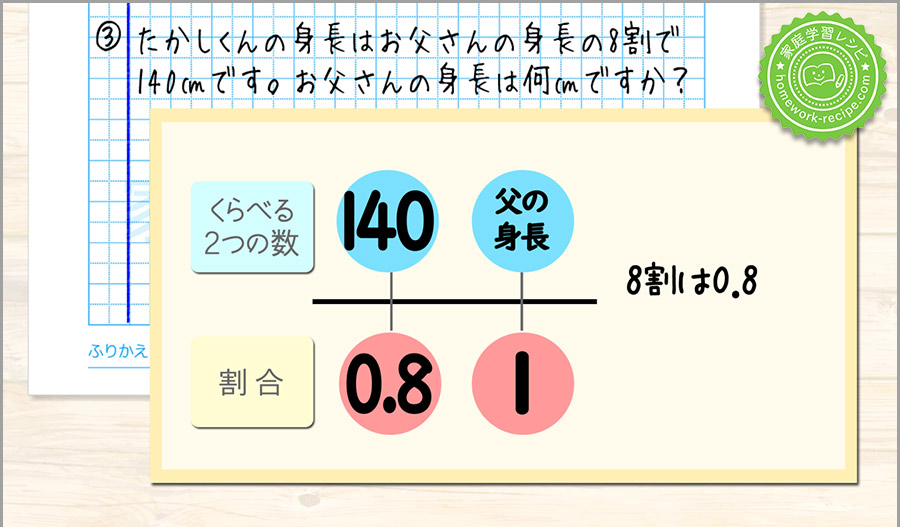
上下の◆に入る数を考えます。
1とみる数の何倍か?を考えるので、今回矢印はこの向きになります。
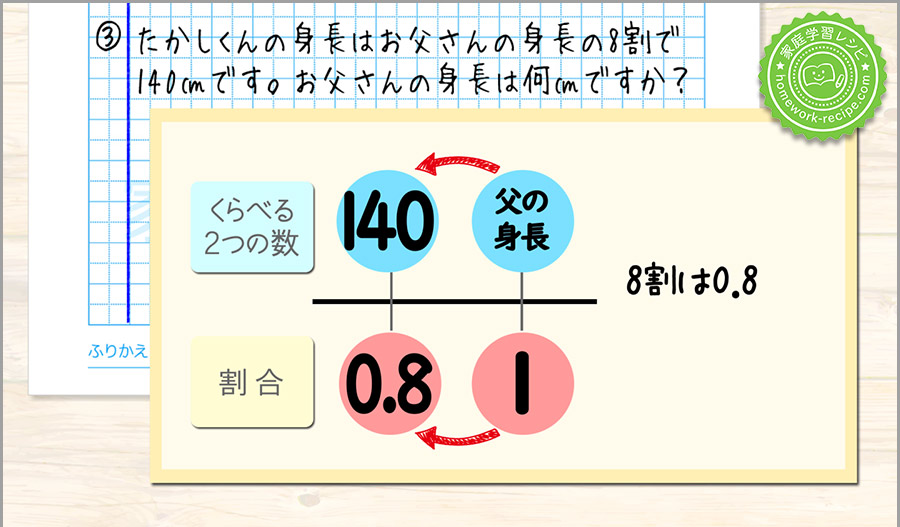
0.8は1の何倍か?を考えると、
0.8÷1=0.8
0.8倍ですね。下の◆には0.8が入ります。
上の◆にも同じく0.8が入ります。
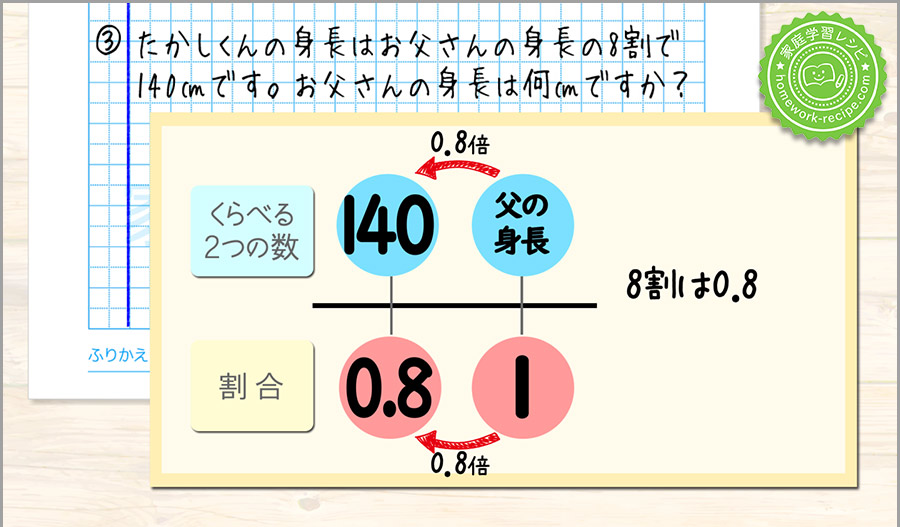
父の身長を□として式を考えるとわかりやすいです。
□の0.8倍が140なので、
□×0.8=140
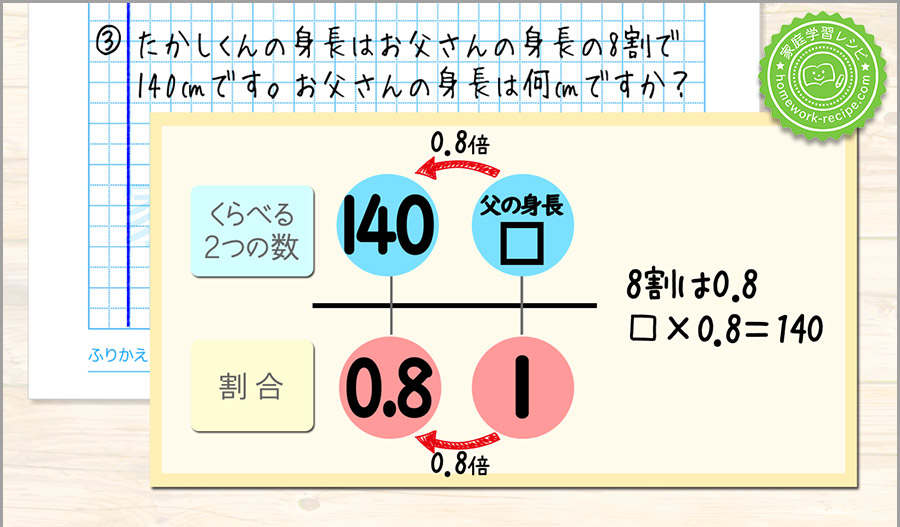
□を求めるには
140÷0.8=175
お父さんの身長は175㎝というのが答えです。
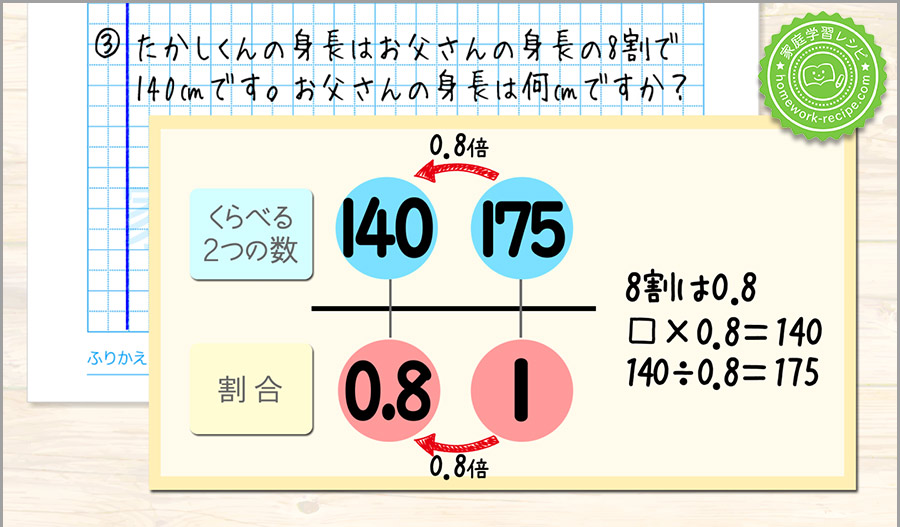
比の問題も同じ図をかいて解ける
このように、比の問題も同じように図をかいて解けます。
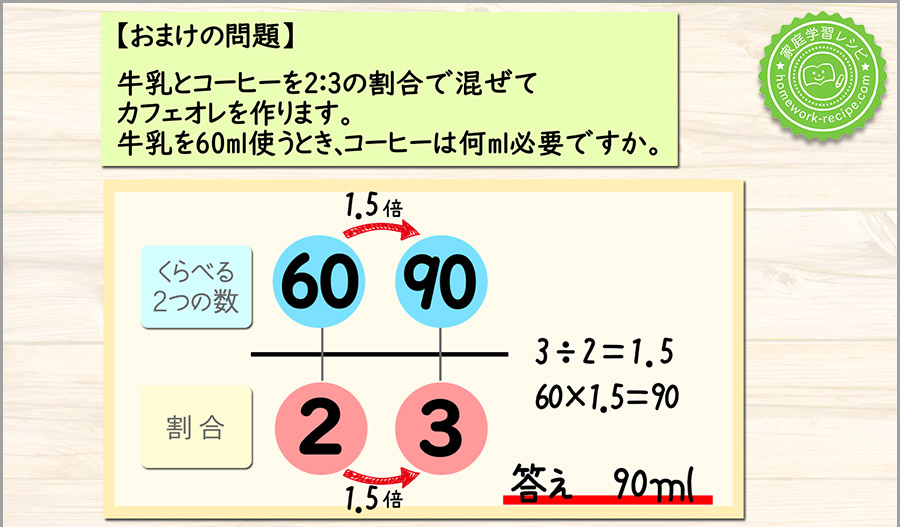
もとにする数を1とした場合の割合以外でも、考え方は同じということです。
この解き方の特徴
- 覚えにくい公式を3つも覚えなくてもいい
- 公式の暗記をして数字を当てはめるだけではなく、線分図をかいて、数を比べるという割合の意味を理解しながら解ける
- 同じやり方で比の問題も解ける
- このやり方の応用で、速さ、濃度、人口密度、割引・割増の問題も解ける
- 学校で習う方法と途中式が同じになる
学校で習う方法とかけ離れた裏技的な解法を、中途半端に教えてしまうと、お子さんが混乱してしまう可能性があります。
それに、宿題や自主勉で、習ったのと違う解き方で解き、先生に「これどうやって解いたの?」と聞かれてお子さんが困ってしまうかもしれません。
今は学校のテストで、途中式や考え方を書かせることが多くなっていますが、学校で習うのと途中式が違っていて、減点されたり×にされたりしてしまう可能性もあります。
このサイトでは、まずは学校で習う方法をしっかり覚えよう、という方針でコンテンツを作っています。
裏技的な解き方もあるにはある
でも実はもっと楽に覚えられて、楽に解ける方法もあるにはあるので、書いておきますね。
図のかき方は同じです。
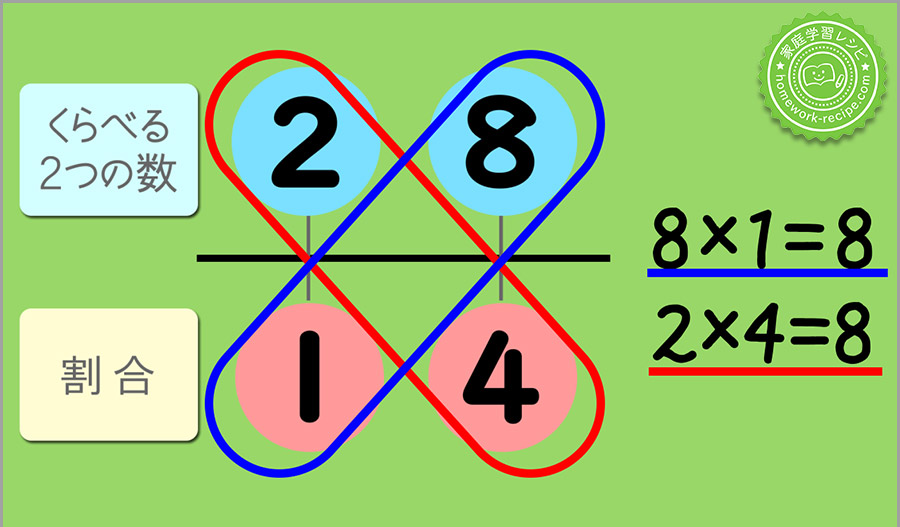
ななめの数字どうしをかけた答えが、同じになります。
これは、2:8=1:4 という比で表すと考えると、中学で習う「比例式の内項の積と外項の積が等しくなる」ということですね。
小学校では習わない考え方ですので、ご利用のさいは自己責任でお願いします。
または、このように割った答えが上下で同じになります。
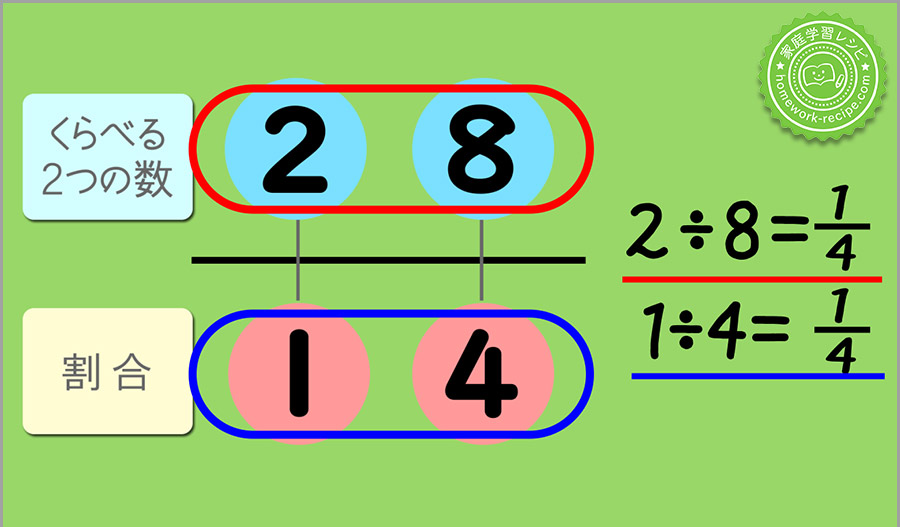
このわり算の答えというのは、これも 2:8=1:4 という比で表した場合の、6年生で習うところの「比の値」のことですね。
こういった性質を覚えておくと、あの覚えにくい公式やくもわの図のような特殊なものを覚えなくても、割合の問題は解けます。
長くなってしまいました。では今日はこのへんで!
動画もよろしくお願いします。
(16分51秒/BGM・ナレーションあり)