割合の問題をとく自主学習【5年算数】
今日は今日は、５～６年生におすすめの、割合の問題をとく自主学習ノートをご紹介します。
割合の基本問題３パターンを、解いてみましょう。
このページの内容を動画でもご覧いただけます。割合の問題を線分図をかいて解く方法を丁寧に解説していますので、ぜひご覧ください。
(16分51秒/BGM・ナレーションあり）
https://youtu.be/miwaIDGJ9G4割合は何年生で習うのか
東京書籍の2020年度からの学習指導要領にもとづいた教科書によると、割合を単元として習うのは５年生ですが、その前に割合の基礎となる「～倍」という考え方を、もっと下の学年から少しずつ学んでいきます。割合という言葉の説明は、４年生の算数の教科書にものっています。
さらに、６年生になると、割合の表し方のひとつとして「比」について学びます。
今回は５年生の自主学習ノート例として作ってみましたが、割合についての自主学習は他の学年の方にもおすすめです。
割合の問題を解く自主学習ノートの作り方
割合の基本問題には３パターンあります。３つの文章題を解いて割合の考え方を確認しましょう。
問題を書き、式や図をかいて、といてみましょう。
よくある割合の解き方
割合の問題には次の３つの要素があります。
- もとにする量
- 比べられる量
- 割合
これを文章題の中から探して、公式にあてはめて計算する、という方法を教えられることが多いと思います。
そもそも、この３つを問題文の中から見つけることが難しいと思うのですが、手掛かりとしては「●の何倍（％、割）」と書かれてあるところがあれば、●がもとにする数です。
割合を求めるには
割合＝比べられる量÷求められる量
比べられる量を求めるには
比べられる量＝もとにする量×割合
もとにする量を求めるには
もとにする量を求めるには、□を使って、
比べられる量＝□（もとにする量）×割合
という式を立てるとわかりやすいです。
□（もとにする量）＝比べられる量÷割合
を計算して求めます。
くもわの図
上の公式がたいそう覚えにくいということで、公式を覚えるためにこのような図が使われることがあります。
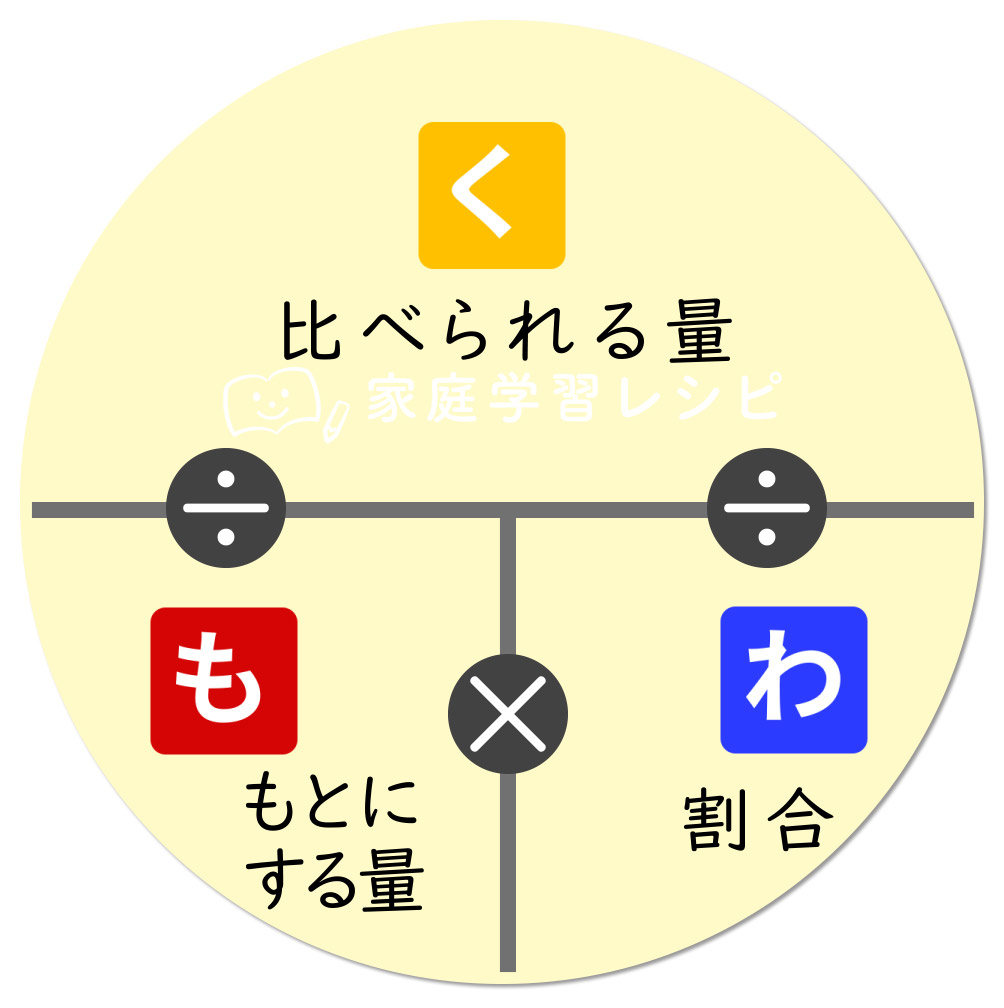
「くもわの図」などと呼ばれるものです。
くもわの図で割合を求める公式を導き出す方法
- 割合以外の二つを使います
- 比べられる量ともとにする量の間にあるのは÷
- 上を下で割ります
割合＝比べられる量÷もとにする量
くもわの図で比べられる量を求める公式を導き出す方法
- 比べられる量以外の二つを使います。
- もとにする量と割合の間にあるのは×なので二つをかけます。
比べられる量＝もとにする量×割合
くもわの図でもとにする量を求める公式を導き出す方法
- もとにする量以外の二つを使います
- 比べられる量と割合の間にあるのは÷
- 上を下で割ります
もとにする量＝比べられる量÷割合
覚えにくい公式を覚えるためのくもわの図ですが、この図の使い方を覚えるのも簡単ではありませんよね…
線分図や考え方を書き、式と答えを書いて、このようにノートを完成させました。
割合の問題のもっとわかりやすい解き方
割合の問題を、もっとシンプルな方法で解くことができます。それについての説明は、ぜひ動画をご覧くださいね。
(16分51秒/BGM・ナレーションあり）
動画の内容を記事にもまとめました。
https://homework-recipe.com/wariai説明は動画の方がわかりやすいと思いますが、動画では説明しきれなかったことも記事には書いています。動画の説明は速すぎると思う方や、一つ一つ確認しながらゆっくり読みたいという方も記事を読んでいただけるとうれしいです。
割合の問題は、中学以降で学ぶ、比例式、相似な図形など数学の基礎ともなります。公式にあてはめて解けるというだけではなく、意味をわかって解けるようになるのが理想です。学校で習ったことを自主学習で復習して、しっかりと身につけましょう。