並べ方と組み合わせ方-その1

並べ方と組み合わせ方についての家庭学習をしてみましょう。樹形図、表、そして辺と対角線の数で考えるなど、組み合わせ方を調べるのには、いろいろな方法があります。
- 組み合わせ方の練習問題を色々な考え方で解こう
どのパターンの問題に、どの解き方が最適かというのはあるのですが、自分でいろんな方法でやってみるうちに、この調べ方が一番速くて確実、と思える方法を見つけられるようになることが大事だと思います。
そこで、2問目は、1つの問題を色々な調べ方で考える問題例としました。
組み合わせの考え方を確認しよう
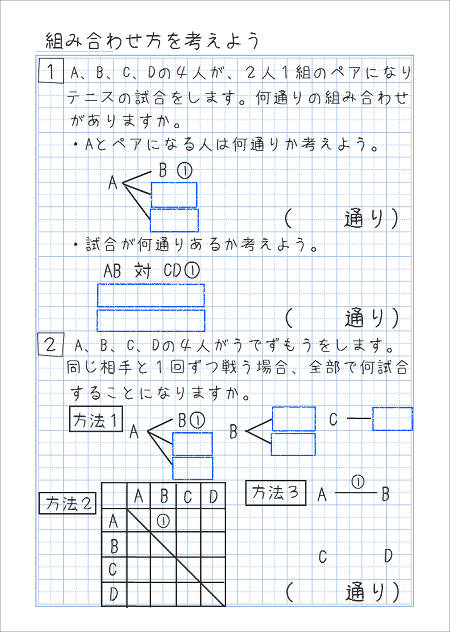
大問を2つやることにしましょう。下の画像のように、問題文や表の枠などを書きます。
ノート1ページにおさめるために、ちょっときゅうくつになりました。もう少しゆったり書いて1ページに1問とし、2ページにわたって勉強してもいいと思います。

2つの大問は、ちょっと読むとなんだか似たような問題ですね。組み合わせ方、並べ方の問題は、このように、パッと見同じようでも、目のつけどころや数え方が違うものが多いので、問題をしっかり読み取る必要があります。
大問1は、Aとペアになる人が決まれば、もう1つのペアも同時に決まるというのがポイントです。Aとペアになる人だけを考えればいい、ともいえます。
でも、そこに気づかなくては解けないというものではありません。
まずは、どういう組み合わせがあるか、思いつくままに書きだしてみるのがいいと思います。思いつくままに書きだしているうちに、そうか「AとBがペア=CとDがペアということなんだな」と気がつくことができればいいのです。
とりあえず、どういう組み合わせがあるか、思いつくままに書いてみる。
組み合わせや並び方の問題で、解法がパッと思い浮かばない時には、これをやってみましょう。
大問2は、いわゆる「総当たり戦」の試合の数を考える問題です。問題集などでは、総当たり戦の表を描いて考えましょう、という解説が多いようですが、これも、いろんな考え方で解けることを知っておくといいと思います。
方法1は、樹形図での考え方です。
方法2は、総当たり戦の表による考え方です。
総当たり戦の表って、見方も描き方も、慣れないと???となると思います。学校でも習うと思いますが、しっかり理解できたでしょうか。
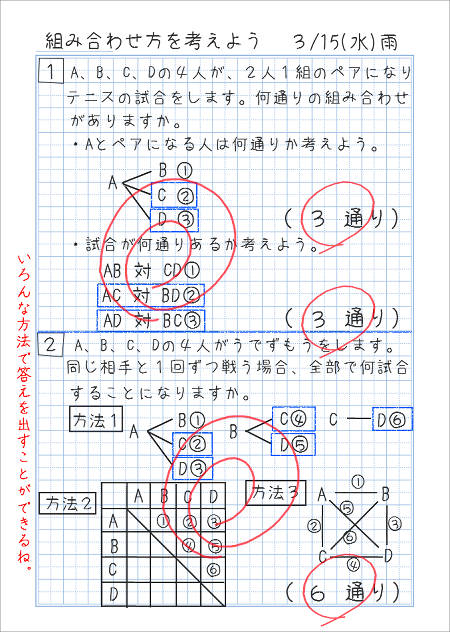
- A対A、B対B等はあり得ないので、斜線で消している。
- 斜線から右斜め上の6マスと、左斜め下の6マスが、だぶっている。
つまり、右斜め上の①と書いた欄が「A対B」とすると、その左斜め下の欄は「B対A」です。この2つは同じことなので、左斜め下の欄は数えません。
といった特徴があるので、見方に気をつけます。
方法3は、辺と対角線を描き、線の数を数える方法です。
学校で習うと思いますので、それぞれの考え方について詳しくは解説しません。そのぶんヒントを多めにしたつもりですが、どうでしょう。
組み合わせ方、並べ方の単元がよくわからないなぁという方は、このノート見本の通りに、難しければ答えの方も見ながら、一度ノートに書いて頂いて、もう一度、次は問題文だけ写して、ヒントなしで解いてみると、なんとなくわかった、という感覚がつかめるのではないでしょうか。

答え合わせをすると、こんな感じに自主学習ノートが仕上がります。
小学生と場合の数
中学校以降の数学で、本格的に、組み合わせや並べ方の学習をします。「場合の数」といって、難しい単元だと思います。中学受験対策として、出題のパターンと解き方を覚え、計算で速く解く方法を勉強したお子さんもいるかもしれませんね。
中学受験しない場合は、小学生のうちは、数えもれがないよう、だぶって数えないよう、間違えることも経験しながら工夫する気持ちを持てたらいいのではないかなという気がします。
いろんな方法で解けるし、どんな方法で解いてもいいのだと思います。
問題にぶつかった時、つまり何が大事なのか、自分でつかめるようになれたらいいですね。
個人的な感想ですが、場合の数を小学生に教えるのは難しそうだなと、このノートを作って思いました。この記事も、説明がわかりにくかったことと思います。
3年生ぐらいから、もっと簡単な組み合わせ方の問題に、少しずつ触れておいた方がいいかもしれませんね。